Improved Aberth-Ehrlich root-finding algorithm and its further application for binary microlensing

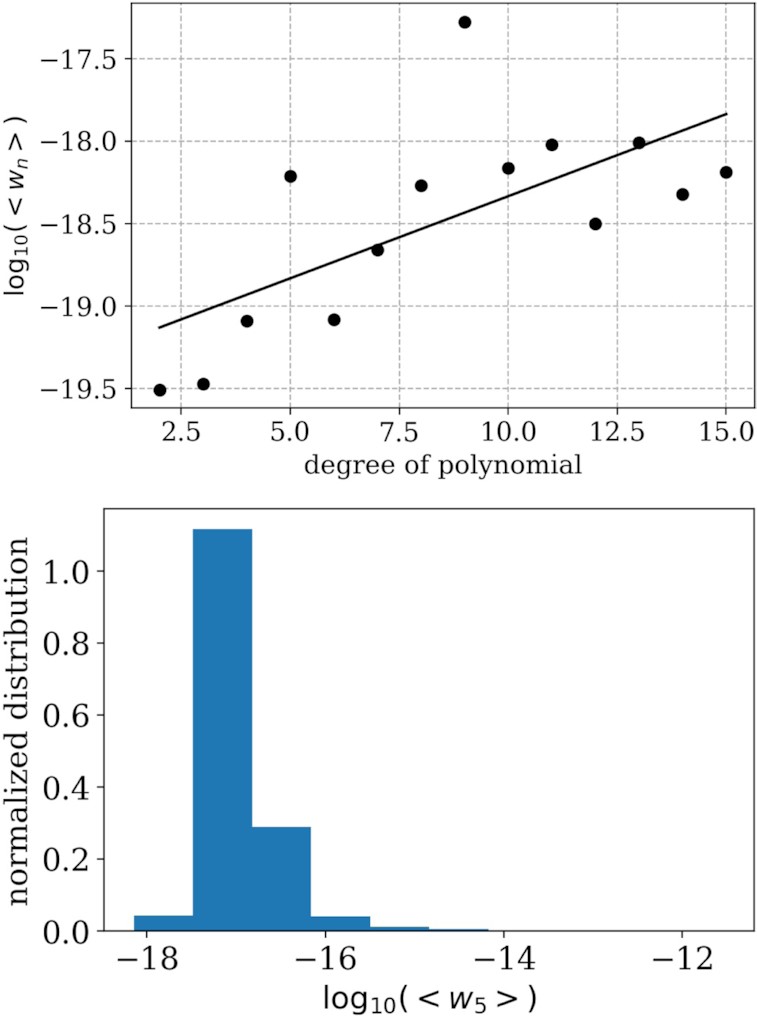
In gravitational microlensing formalism and for modelling binary light curves, the key step is solving the binary lens equation. Currently, a combination of the Newton's and Laguerre's methods which was first introduced by Skowron & Gould (SG) is used while modelling binary light curves. In this paper, we first introduce a fast root-finding algorithm for univariate polynomials based on the Aberth-Ehrlich (AE) method which was first developed in 1967 as an improvement over the Newton's method. AE algorithm has proven to be much faster than Newton's, Laguerre's, and Durand-Kerner methods and unlike other root-finding algorithms, it is able to produce all the roots simultaneously. After improving the basic AE algorithm and discussing its properties, we will optimize it for solving binary lens equations, which are fifth degree polynomials with complex coefficients. Our method is about 1.8-2.0 times faster than the SG algorithm. Since, for calculating magnification factors for point-like or finite source stars, it is necessary to solve the binary lens equation and find the positions of the produced images in the image plane first, this new method will improve the speed and accuracy of binary microlensing modelling.