A New HLLD Riemann Solver with Boris Correction for Reducing Alfvén Speed

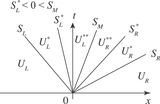
A new Riemann solver is presented for the ideal magnetohydrodynamics (MHD) equations with the so-called Boris correction. The Boris correction is applied to reduce wave speeds, avoiding an extremely small timestep in MHD simulations. The proposed Riemann solver, Boris-HLLD, is based on the HLLD solver. As done by the original HLLD solver, (1) the Boris-HLLD solver has four intermediate states in the Riemann fan when left and right states are given, (2) it resolves the contact discontinuity, Alfvén waves, and fast waves, and (3) it satisfies all the jump conditions across shock waves and discontinuities except for slow shock waves. The results of a shock tube problem indicate that the scheme with the Boris-HLLD solver captures contact discontinuities sharply, and it exhibits shock waves without any overshoot when using the minmod limiter. The stability tests show that the scheme is stable when | u| ≲ 0.5c for a low Alfvén speed ({V}_A≲ c), where u, c, and V _A denote the gas velocity, speed of light, and Alfvén speed, respectively. For a high Alfvén speed ({V}_A≳ c), where the plasma beta is relatively low in many cases, the stable region is large, | u| ≲ (0.6{--}1)c. We discuss the effect of the Boris correction on physical quantities using several test problems. The Boris-HLLD scheme can be useful for problems with supersonic flows in which regions with a very low plasma beta appear in the computational domain.