Breaking black-hole uniqueness at supermassive scales
Abstract
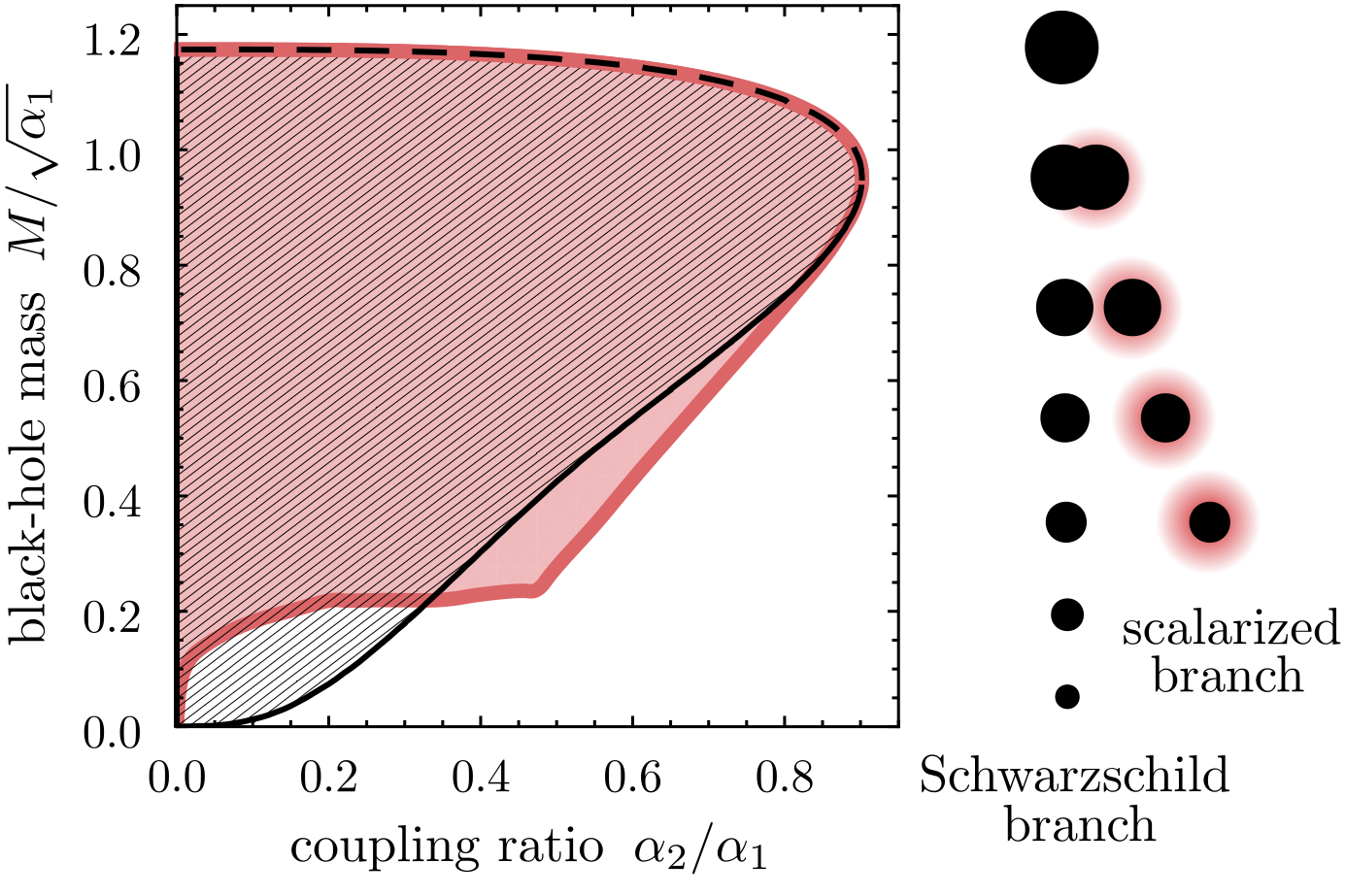
In general relativity, all vacuum black holes are described by the Kerr solution. Beyond general relativity, there is a prevailing expectation that deviations from the Kerr solution increase with the horizon curvature. We challenge this expectation by showing that, in a scalar-Gauss-Bonnet theory, black holes scalarize in a finite, adjustable window of black-hole masses, bounded from above and below. In this theory, there is an interplay between curvature scales and compactness, which we expect to protect neutron stars and other less compact objects from scalarization. In addition, this theory is the first to avoid the catastrophic instability of early-universe cosmology that affects previous scalarization models. In this theory, black-hole uniqueness can be broken at supermassive black-hole scales, while stellar-mass black holes remain well-described by the Kerr solution. To probe this scenario, observations targeting supermassive black holes are necessary.
- Publication:
-
arXiv e-prints
- Pub Date:
- December 2023
- DOI:
- arXiv:
- arXiv:2312.11430
- Bibcode:
- 2023arXiv231211430E
- Keywords:
-
- General Relativity and Quantum Cosmology;
- Astrophysics - High Energy Astrophysical Phenomena;
- High Energy Physics - Theory
- E-Print:
- 6 pages, 3 figures + supplemental material