Variations on the theme of Michel Henon's Isochrone
Abstract
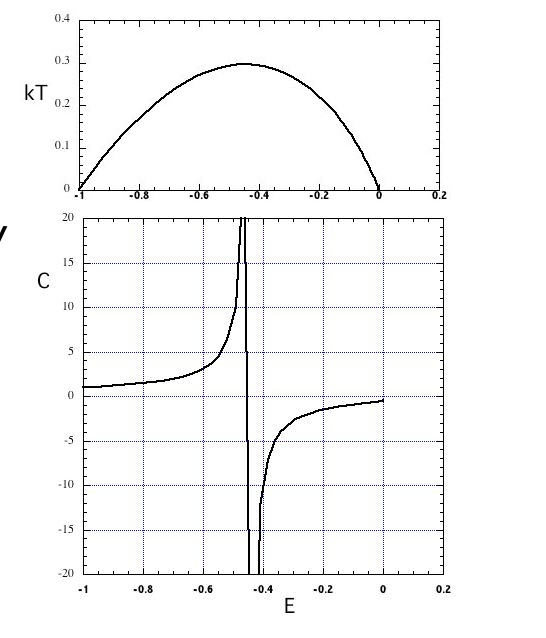
A variation of Newton's method of mapping Kepler's orbits into orbits in the simple harmonic oscillator is shown to give Henon's Isochrone. The statistical mechanics of a micro-canonical ensemble of isochrone oscillators shows that the temperature reaches a maximum as a function of the energy and then declines to zero at the escape energy. In that declining region adding heat (energy) decreases the temperature, as occurs in star clusters. We then define the internal temperature of an ensemble of binary stars all at the same (negative) energy and show that they too get cooler when heated and hotter when cooled. When the internal temperature of a binary is less that the temperature of the stars it interacts with, then on average heat will flow into it, making it less bound and of still lower temperature. Conversely hard binaries have higher internal temperatures than the local stars, so they lose energy and become hotter and yet more strongly bound, a process invoked by Michel Henon in his explanation of star-cluster evolution. Finally we give an isochronal variation of Newton's exactly soluble N-body problem.
- Publication:
-
arXiv e-prints
- Pub Date:
- November 2014
- DOI:
- 10.48550/arXiv.1411.4926
- arXiv:
- arXiv:1411.4926
- Bibcode:
- 2014arXiv1411.4926L
- Keywords:
-
- Astrophysics - Astrophysics of Galaxies
- E-Print:
- Invited talk at the "hommage a Michel Henon" conference held at the "Institut Henri Poincare" Paris, GRAVASCO trimestre, autumn 2013. Proceeding by Hermann Press, editors: Jean-Michel Alimi, Roya Mohayaee, Jerome Perez. Videos of all talks are available at: https://www.youtube.com/playlist?list=PL9kd4mpdvWcBLrN8u04IZW6-akNgLG7-_