Evolution of skewness and kurtosis of cosmic density fields

Aims: We investigate the evolution of the one-point probability distribution function (PDF) of the dark matter density field and the evolution of its moments for fluctuations that are Gaussian in the linear regime.
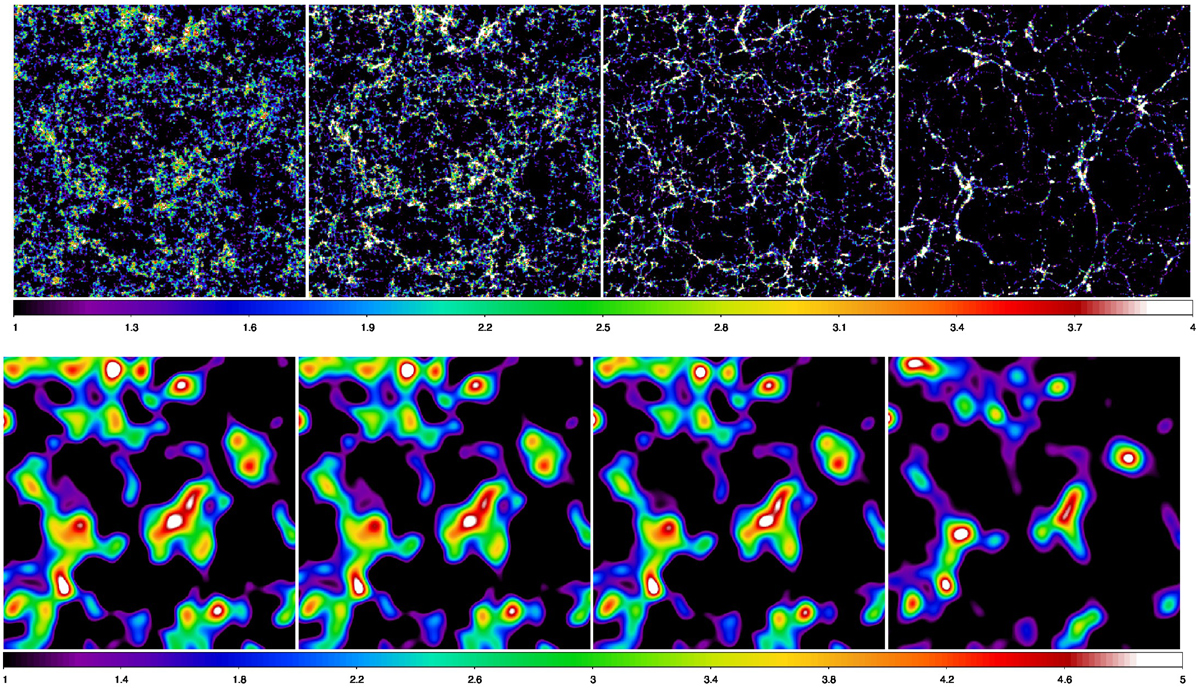
Methods: We performed numerical simulations of the evolution of the cosmic web for the conventional ΛCDM model. The simulations covered a wide range of box sizes L = 256 − 4000 h⁻¹ Mpc, mass, and force resolutions, and epochs from very early moments z = 30 to the present moment z = 0. We calculated density fields with various smoothing lengths to determine the dependence of the density field on the smoothing scale. We calculated the PDF and its moments variance, skewness, and kurtosis. We determined the dependence of these parameters on the evolutionary epoch z, on the smoothing length R_t, and on the rms deviation of the density field σ using a cubic-cell and top-hat smoothing with kernels 0.4 h⁻¹ Mpc ≤ R_t ≤ 32 h⁻¹ Mpc.
Results: We focus on the third (skewness S) and fourth (kurtosis K) moments of the distribution functions: their dependence on the smoothing scale R_t, the amplitude of the fluctuations σ, and the redshift z. Moments S and K, calculated for density fields at different cosmic epochs and smoothed with various scales, characterise the evolution of different structures of the web. Moments calculated with small-scale smoothing (R_t ≈ (1 − 4) h⁻¹ Mpc) characterise the evolution of the web on cluster-type scales. Moments found with strong smoothing (R_t ≳ (5 − 15) h⁻¹ Mpc) describe the evolution of the web on supercluster scales. During the evolution, the reduced skewness S₃ = S/σ and reduced kurtosis S₄ = K/σ² present a complex behaviour: at a fixed redshift, curves of S₃(σ) and S₄(σ) steeply increase with σ at σ ≲ 1 and then flatten out and become constant at σ ≳ 2. When we fixed the smoothing scale R_t, the curves at large σ started to gradually decline after reaching the maximum at σ ≈ 2. We provide accurate fits for the evolution of S_{3, 4}(σ, z). Skewness and kurtosis approach constant levels at early epochs S₃(σ)≈3 and S₄(σ)≈15.
Conclusions: Most of the statistics of dark matter clustering (e.g. halo mass function or concentration-mass relation) are nearly universal: they mostly depend on the σ with a relatively modest correction to apparent dependence on the redshift. We find just the opposite for skewness and kurtosis: the dependence of the moments on the evolutionary epoch z and smoothing length R_t is very different. Together, they uniquely determine the evolution of S_{3, 4}(σ). The evolution of S₃ and S₄ cannot be described by current theoretical approximations. The often used lognormal distribution function for the PDF fails to even qualitatively explain the shape and evolution of S₃ and S₄.