Detection of periodicity based on independence tests - III. Phase distance correlation periodogram

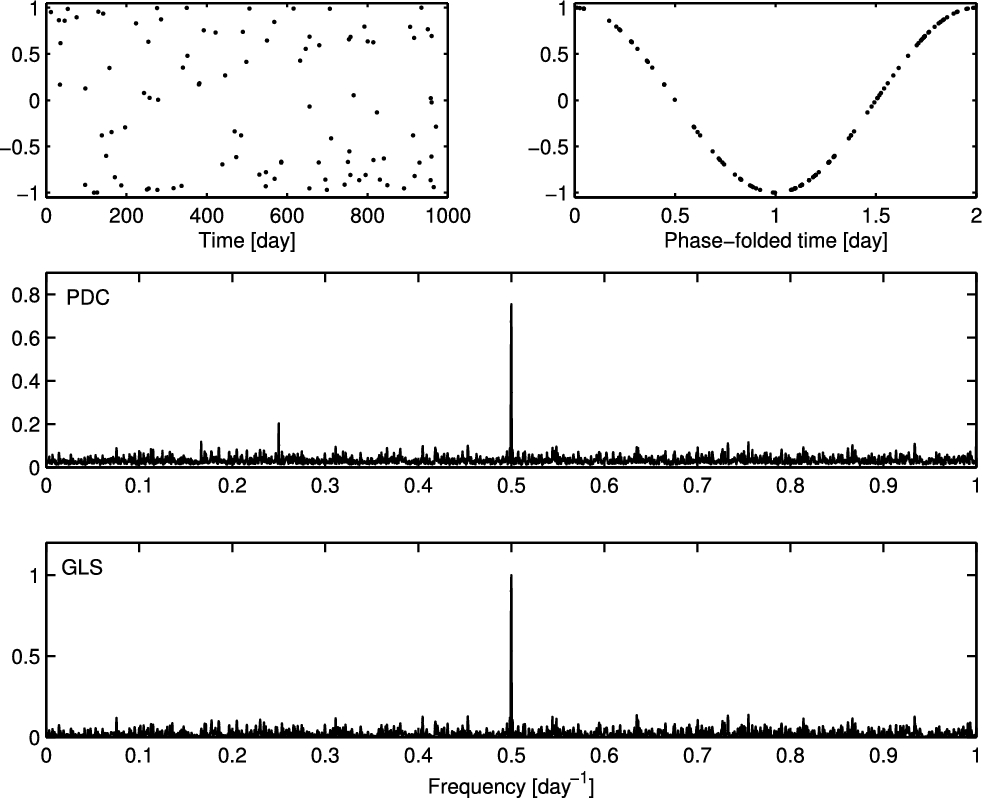
I present the Phase Distance Correlation (PDC) periodogram - a new periodicity metric, based on the Distance Correlation concept of Gábor Székely. For each trial period, PDC calculates the distance correlation between the data samples and their phases. PDC requires adaptation of the Székely's distance correlation to circular variables (phases). The resulting periodicity metric is best suited to sparse data sets, and it performs better than other methods for sawtooth-like periodicities. These include Cepheid and RR-Lyrae light curves, as well as radial velocity curves of eccentric spectroscopic binaries. The performance of the PDC periodogram in other contexts is almost as good as that of the Generalized Lomb-Scargle periodogram. The concept of phase distance correlation can be adapted also to astrometric data, and it has the potential to be suitable also for large evenly spaced data sets, after some algorithmic perfection.